대수의 법칙과 중심극한정리

📜 1. 대수의 법칙 (Law of Large Numbers, LLN)

대수의 법칙이란?

• 표본의 크기(관찰 횟수)가 커질수록 표본 평균은 모집단의 평균에 수렴한다.
• 반복 측정을 통해 불확실성을 줄이고 안정적인 평균 추정 가능

💡 예시 (동전 던지기)

• 앞면을 1, 뒷면을 0으로 가정
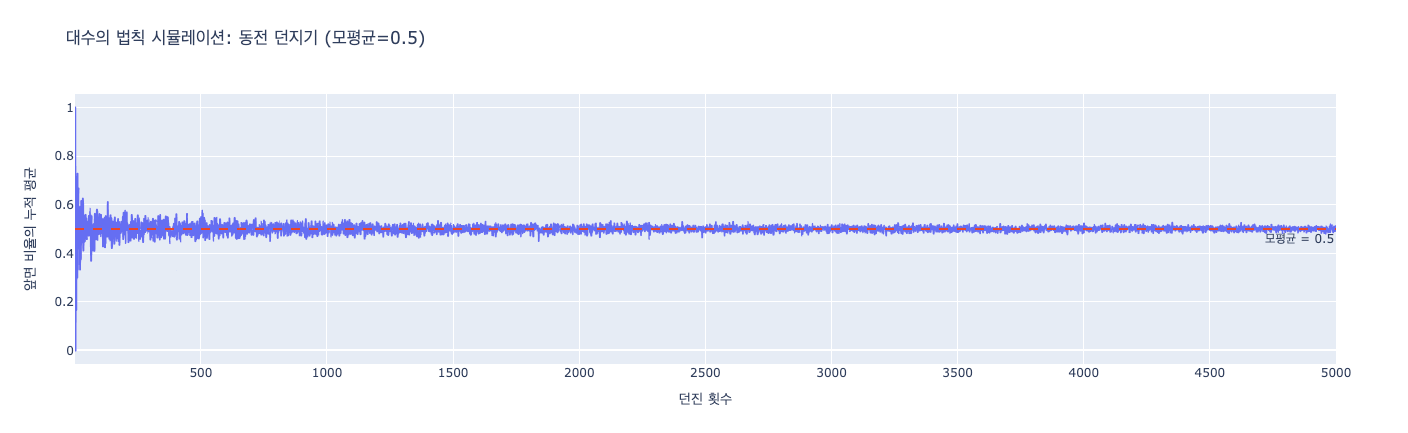
• 반복 횟수를 늘릴수록 표본 평균이 0.5(모평균)에 가까워짐

# np.random.binomial(1, p, size)
#   => 한 번의 시도에서 성공 확률이 p인 베르누이 시행을 size만큼 반복
trials = np.random.binomial(1, 0.5, n)
sample_mean = np.mean(trials)

실행 결과

📌 2. 중심극한정리 (Central Limit Theorem, CLT)

중심극한정리란?

• 통계학에서 가장 강력하고 놀라운 아이디어 중 하나
• 모집단 분포가 어떠하든, 표본 크기가 충분히 크면 표본 평균 분포는 정규분포에 가까워진다.
  • 일반적으로 표본 크기 n ≥ 30이면 성립
• 표본 평균의 분포는 예측 가능한 정규분포를 따르기 때문에 통계적 추론(예: 신뢰구간 추정, 가설 검정)을 할 수 있게 됨

• 핵심 아이디어:
  1. 모집단에서 크기 n의 표본을 여러 번 추출
  2. 각 표본에서 표본 평균을 계산
  3. 이렇게 얻은 수많은 표본 평균들의 분포는 정규분포를 따르게 됨
  4. 이때 다음이 성립:
     • 표본 평균 분포의 평균 = 모집단 평균 μ
     • 표본 평균 분포의 분산 = 모집단 분산 σ² / n
     • 표본 평균 분포의 표준편차 (표준오차) = σ / √n

즉, 표본 크기가 커질수록 표본 평균 분포는 정규분포 형태로 수렴하며 분산이 작아져 더 정밀한 추정이 가능

💡 예시 (균일 분포 → 표본 평균 정규화)

• 표본 평균 분포는 정규분포 형태로 수렴

population = np.random.uniform(0, 1, 100000)
sample = np.random.choice(population, size=30, replace=True)
sample_mean = np.mean(sample)

실행결과

• 모집단 분포 그래프: 균일 분포이므로, 0과 1 사이에서 거의 평평한 모양의 히스토그램이 나타남

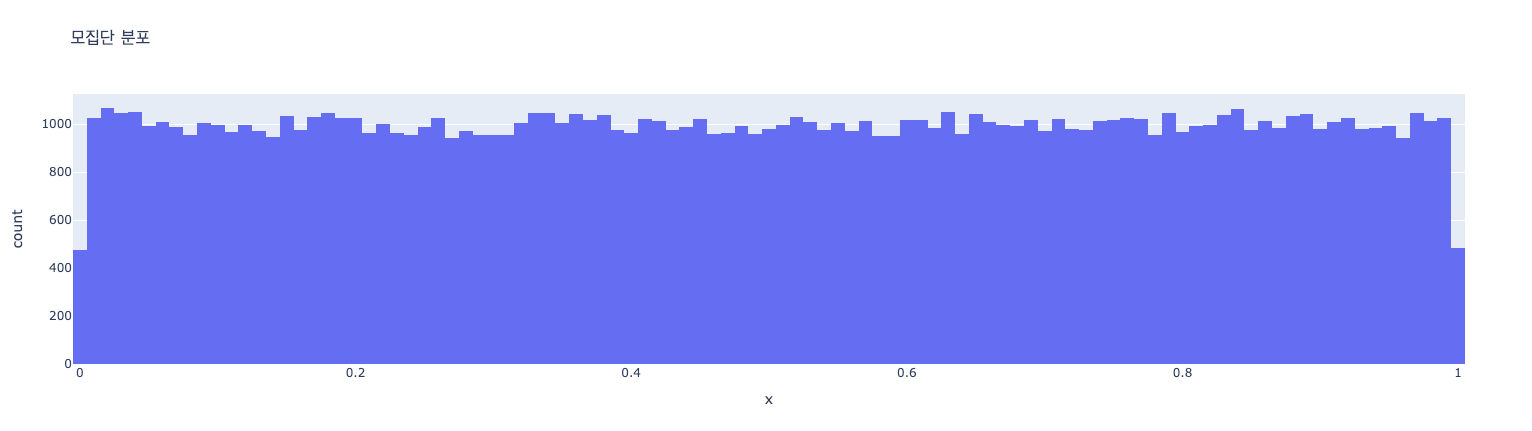
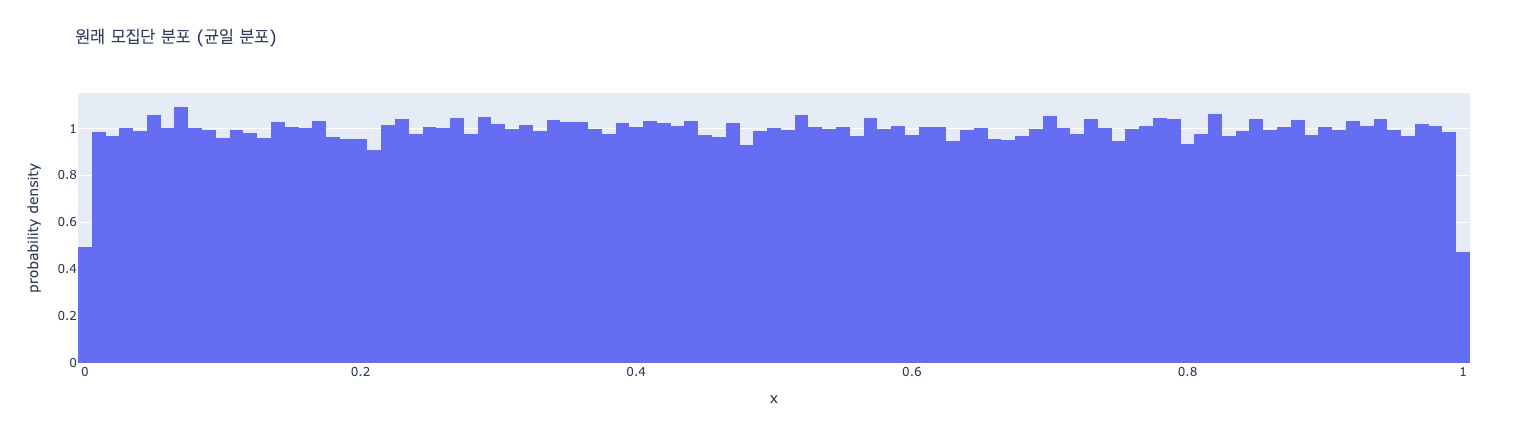
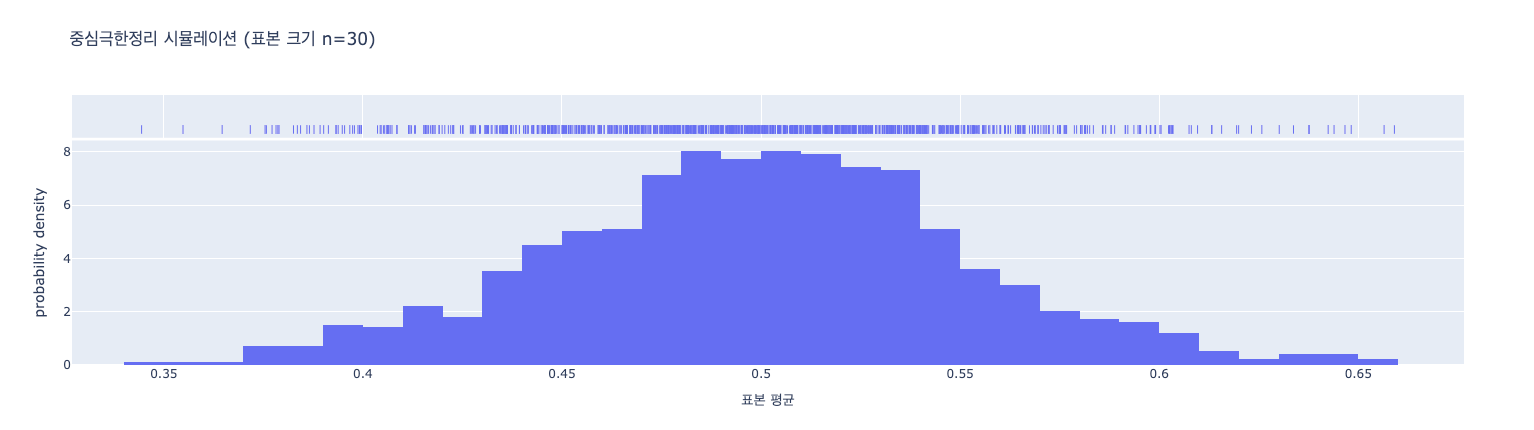
• 표본 평균 분포 그래프: 종 모양(정규분포와 유사한 모양). 원래 모집단이 균일 분포였음에도 불구하고, 표본 평균들의 분포는 중심극한정리에 따라 정규분포에 가까워지는 것을 확인할 수 있음

✏️ 실습 과제

• 지수 분포(Exponential Distribution)를 모집단으로 설정하고, 중심극한정리가 실제로 나타나는지 시뮬레이션으로 확인
• 지수 분포는 오른쪽으로 꼬리가 긴 비대칭 분포
• 다양한 표본 크기(예: n=2, n=10, n=30, n=100)에 대해 표본 평균의 분포가 어떻게 변하는지 관찰하고 설명

1. numpy.random.exponential(scale=…, size=…) 함수를 사용하여 지수 분포를 따르는 모집단을 생성합니다. (예: scale=1, size=100000)
   • 지수 분포의 평균은 scale 값과 같습니다.
   • 지수 분포의 표준편차도 scale 값과 같습니다.

from scipy import stats
import numpy as np
pop = stats.expon.rvs(scale=1, size=100000)
pop

sample_means = []
for _ in range(1000):
    sample = np.random.choice(pop, size=100, replace=True)
    sample_means.append(np.mean(sample))

print("모집단 평균: ", np.mean(pop))

1. 각 표본 크기 (sample_sizes = [2, 10, 30, 100])별로 다음을 반복합니다:
   • 모집단에서 해당 sample_size만큼의 표본을 1000번 추출합니다.
   • 각 표본의 평균을 계산하여 저장합니다.

sample_sizes = [2, 10, 30, 100]
sample_dict = {
    sample_size: [stats.expon.rvs(scale=1, size=sample_size) for _ in range(1000)]
    for sample_size in sample_sizes
}

sample_dict

1. 각 표본 크기별로 수집된 표본 평균들의 분포를 Plotly Express를 사용하여 히스토그램으로 시각화합니다 (histnorm=’probability density’ 사용).
   • 각 그래프의 제목에 사용된 표본 크기를 명시합니다.
   • 원래 모집단(지수 분포)의 히스토그램도 함께 그려서 비교해보면 좋습니다.

1. 마크다운 셀에 다음 내용을 포함하여 결과를 설명합니다:
   • 원래 모집단(지수 분포)의 모양은 어떠한가?
   • 표본 크기가 증가함에 따라 표본 평균의 분포 모양은 어떻게 변하는가? 중심극한정리가 관찰되는가?
   • 각 표본 평균 분포의 평균은 모집단 평균에 가까워지는가?
   • 표본 크기가 커질수록 표본 평균 분포의 표준편차(표준오차)는 어떻게 변하는가? 이론값(σ / √n)과 비교해볼 수 있다면 더욱 좋습니다.

• 힌트:
  • np.random.exponential() 함수의 scale 파라미터는 λ의 역수 (scale = 1/λ)이며, 이 분포의 평균과 표준편차는 모두 scale 값과 같습니다.
  • 튜토리얼의 중심극한정리 시뮬레이션 코드를 참고하여 여러 표본 크기에 대한 반복문 구조를 추가합니다.
  • Plotly의 facet_col 또는 facet_row 옵션을 사용하거나, 여러 개의 fig.show()를 호출하여 여러 그래프를 한 번에 또는 순차적으로 볼 수 있습니다.

Data-Analytics 카테고리 내 다른 글 보러가기

첫 번째 글입니다 가장 최근 글입니다